Đề thi và đáp án tuyển sinh lớp 10 năm 2021-2022 - môn Toán

26.06.2021 11:37 |

5.320

Đề thi vào lớp 10 môn Toán Đồng Nai năm 2021

Đáp án đề thi vào lớp 10 môn Toán Đồng Nai năm 2021

Câu 1: (2 điểm)

1) Giải phương trinh $x^{2}+3 x-10=0$

Ta có: $\Delta=3^{2}-4 \cdot(-10)=49>0$ nên phương trình có 2 nghiệm phân biệt $\left[\begin{array}{l}x_{1}=\frac{-3+\sqrt{49}}{2}=2 \\ x_{2}=\frac{-3-\sqrt{49}}{2}=-5\end{array}\right.$

Vậy tập nghiệm của bất phương trình là $S=\{2 ;-5\}$ .

2) Giải phương trình $3 x^{4}+2 x^{2}-5=0$

Đặt $t=x^{2}(t \geq 0)$ , phương trình đã cho trở thành $3 t^{2}+2 t-5=0$ .

Ta có $a+b+c=2+3-5=0$ nên phương trình có 2 nghiệm phân biệt $\left[\begin{array}{l}t_{1}=1(\mathrm{tm}) \\ t_{2}=\frac{c}{a}=-\frac{5}{3}(\mathrm{ktm})\end{array}\right.$ .

Với $t=1 \Rightarrow x^{2}=1 \Leftrightarrow x=\pm 1$ .

Vậy tập nghiệm của phương trình .

3) Giải hệ phương trình $\left\{\begin{array}{l}2 x-3 y=1 \\ x+2 y=4\end{array}\right.$

Ta có: $\left\{\begin{array}{l}2 x-3 y=1 \\ x+2 y=4\end{array} \Leftrightarrow\left\{\begin{array}{l}2 x-3 y=1 \\ 2 x+4 y=8\end{array} \Leftrightarrow\left\{\begin{array}{l}7 y=7 \\ x=4-2 y\end{array} \Leftrightarrow\left\{\begin{array}{l}y=1 \\ x=2\end{array}\right.\right.\right.\right.$

Vậy hệ phương trình có nghiệm $(x ; y)=(2 ; 1)$ .

Câu 2: (2,25 điểm)

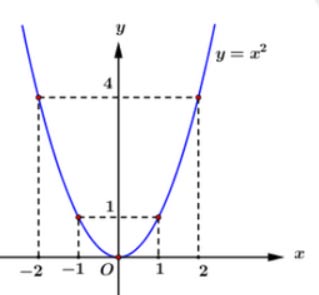
1. Vẽ đồ thị hàm số (P): y = x²

Parabol (P): y = x²có bề lõm hướng lên và nhận Oy làm trục đối xứng

Ta có bảng giá trị sau:

x	-2	-1	0	1	2
y = x²	4	1	0	1	4

⇒ Parabol (P): y = x² đi qua các điểm (-2;4), (-1,1); (0;0), (1;1), (2,4)

Đồ thị Parabol (P): y = x²:

Đồ thị Parabol

2) Tìm giá trị của tham số thực m để Parabol (P): y = x²và đường thẳng $(d): y=2 x-3 m$ có đúng một điểm chung.

Xét phương trình hoành độ giao điểm của (P), (d) ta được:

$x^{2}=2 x-3 m \Leftrightarrow x^{2}-2 x+3 m=0 \text { (1) }$

Để (P) cắt (d) có đúng một điểm chung khi và chi khi (1) có nghiệm kép

$\Leftrightarrow \Delta^{\prime}=0 \Leftrightarrow 1-3 m=0 \Leftrightarrow m=\frac{1}{3}$

Vậy $m=\frac{1}{3}$ thỏa mãn yêu cầu bài toán.

3) Cho phương trình $x^{2}+5 x-4$ . Gọi $x_{1}, x_{2}$ là hai nghiệm phân biệt của phương trình, hãy tinh giả trị của biểu thức $Q=x_{1}^{2}+x_{2}^{2}+6 x_{1} x_{2}$

Vì $x_{1}, x_{2}$ là hai nghiệm phân biệt của phương trình đã cho nên áp dụng hệ thức Vi-et với phương trình $x^{2}+5 x-4=0$ ta có: $\left\{\begin{array}{l}x_{1}+x_{2}=-5 \\ x_{1} x_{2}=-4\end{array}\right.$ .